3. Block Padding
Most messages do not divide neatly into the
fixed-size blocks required by the cipher function, and there is
usually a partial data block left over at the end. The
cipher function cannot process partial
blocks, and the algorithm adds
"padding" to the leftover data to
create a complete block.
Padding, unlike other aspects of encryption, is expressed in bytes
rather than bits. For example, if you are using a cipher that
processes 64-bit blocks, a 13-byte (104-bit) message breaks down into
one complete data block with 40 bits remaining. We need to add 3
bytes (24 bits) of data to the remainder to create a second block
that the cipher function can process. There are two commonly used
approaches to block padding, and the .NET Framework supports both.
The first approach is simply to set the remaining bytes to 0, as
shown in Figure 8.
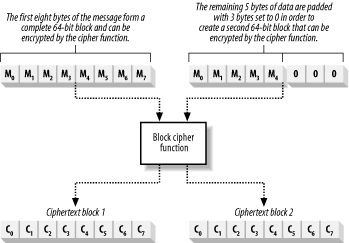
Encrypt the padded plaintext block, and the result is appended to the
ciphertext; note that the ciphertext will be three bytes larger than
the plaintext. When you decrypt the ciphertext, remove the padding
values to return to the original plaintext message. The problem with
this approach is that it is difficult to be sure that you are
removing the padding correctly; some algorithms naturally generate
strings of zeros, and you may remove bytes that are part of the
message.
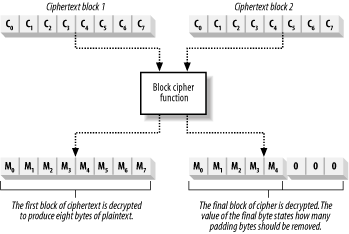
A more reliable approach is to use PKCS #7 padding, where you set the value
of the padding bytes to the number of bytes you added. For our
example, the padding would be three bytes set to a value of
"3". When you remove the padding,
simply read the value of the last byte and you can tell which bytes
you have to remove, as shown in Figure 9.
You still have to add PKCS #7 padding even when there are no partial
plaintext blocks to process. This is because many algorithm
implementations examine the numeric value of the last byte, and do
not check to ensure that all of the padding bytes are set to the same
value. When the plaintext results in only whole blocks, add a
complete block of padding data, with all of the byte values set to be
1/8th of the block size; for a 64-bit block cipher, this would be 8
bytes of value "8". When the
ciphertext is decrypted, remove the entire final block to leave the
original plaintext. PKCS #7 padding is limited to 256 bytes of
padding, which is the largest numeric value a single byte of data can
represent.
4. Symmetric Encryption Key Lengths
The security of symmetric encryption
comes from the fact that Eve does not have the secret key. If she
did, she would be able to read any of Alice's
messages to Bob and even forge new messages by using the secret key
to encrypt them.
We describe secret keys by their length, measured in bits. A 64-bit
key can represent 264 different key
values, and a 256-bit key can represent
2256
different key
values. Symmetric encryption keys are typically attacked using brute
force, where Eve tries all of the possible keys until she finds the
one that Alice and Bob have selected. Protect the confidential
messages by making it hard for Eve to try all of the possible keys;
the longer you make the key, the longer it takes Eve to check all of
the possible key values.
|
When you see calculations that tell you how long it
takes to guess a secret key, you should be aware of two assumptions
that are rarely stated:
Alice and Bob select the secret key randomly, and Eve has no
information that would lead her to suspect that checking a specific
range of keys is more likely to yield a result than any other range. Eve will have to check all of the possible key values before she
finds the correct one.
If you consider these assumptions, you will notice that there is a
fundamental conflict. For a randomly selected key, Eve may be lucky
and find that the first key that she checks is the one that she is
looking for.
It will take Eve 11.6 billion years to try all
the possible values for a 64-bit key if she can test 50 keys per
second, but there is a 50% chance that she will find a match after
checking only half the key space and a 1 in
264 chance that the first key she checks
will be the one that Alice and Bob have used. When assessing the
security of keys, always bear in mind that brute force attacks are
subject to the laws of probability, and it's a very
optimistic expectation to hope that Eve will have to check all
possible keys.
If Eve knows that the key is contained in a specific range, then the
situation is even worse: not only is early success still possible but
she is also able to reduce the total number of keys to check.
|
Assess the length of the key you need by estimating how many
candidate keys Eve can test per second then compare this with how
long you need to maintain confidentiality. For example, if Eve could
check 50 candidate keys per second, it would take her 11.6 billion
years to check all of the possible values for a 64-bit key. If Eve checks more keys per second,
then you will have to adjust your projections accordingly.
The trade-off is that encrypting and decrypting data using longer
keys requires more computation, and using very long keys is practical
only when you are using high-end computers. Make a reasonable
estimate of your confidentiality requirements when selecting a key
length and include an estimation of how Eve's
ability to perform brute force attacks will change over time. History
shows us that improvements in design and manufacturing halve the cost
of processing power every 18 months; therefore, over time Eve will be
able to increase her ability to check candidate keys for each dollar
that she spends.
5. The .NET Framework Encryption Algorithms
The .NET Framework provides classes for four
different symmetric encryptions. Table 1
summarizes the encryption algorithms available and the possible
secret key lengths.
Table 1. Summary of .NET symmetric encryption algorithms
|
Name
|
Block size
|
Key length (bits)
|
|---|
|
DES
|
64
|
56 (although conventionally expressed as a 64-bit number)
|
|
RC2
|
64
|
40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, 128
|
|
Triple-DES
|
64
|
Two or three 56-bit keys, expressed as 64-bit numbers
|
|
Rijndael (AES)
|
128, 192, 256
|
128, 192, 256
|
Based on the Lucifer cipher developed by IBM, the
Data Encryption
Standard (DES) algorithm was published in 1976 and has been used in a
huge range of applications. The design has aged remarkably well,
given it's rocky beginnings. To produce DES, the
National Security Agency modified the Lucifer cipher in a way that
was thought to compromise security. (A common theory throughout
recent cryptographic history is that the National Security Agency is
tinkering behind the scenes to limit the efficacy of cryptography.)
The limit of a 56-bit key means that DES is becoming increasingly
susceptible to exhaustive key searches using modern computers, but
various efforts have been made to prolong the life of this venerable
cipher, most notably the Triple-DES standard. The Advanced Encryption
Standard (AES) officially succeeded DES in 2001 as the principal U.S.
federal standard for data encryption.
The RC2
algorithm was developed by Ron Rivest of RSA
as a direct replacement for DES. Controversy dogged the acceptance of
RC2, because RSA decided to keep the details of the cipher secret,
preventing proper security analysis. In 1997, RSA published the
details of the algorithm to foster the adoption of the S/MIME
standard, which acts as a framework for cryptographically secure
email. A wide range of products use RC2, and it has become one of the
most commonly used symmetrical ciphers. RC2 operates with key lengths
ranging from 40 to 128 bits.
Designed to prolong the life of DES, Triple-DES encrypts data three times
using the DES algorithm. A different 56-bit key can be used for each
encryption step, or two 56-bit keys can be used and the third
encryption step will be performed using the first key. Triple-DES has
found a lasting niche in the international financial markets for
encrypting banking data.
Rijndael (pronounced
"RAIN-Dahl" or
"REIN-Daal") was the winner of the
U.S. Government's selection process for the AES,
which is the successor to the aging DES algorithm. Unlike the other
algorithms included in the .NET Framework, the Rijndael cipher
function operates on a range of data block sizes. Although tested
rigorously during selection, cryptographers have not yet established
the long-term security of the Rijndael/AES algorithm. You should
exercise caution before using Rijndael, and remember that it takes a
great deal of time and analysis before a new algorithm can be fully
trusted.