A hashing
algorithm creates a hash code, also called a
"message digest" or
"message fingerprint." Hash codes are of limited
use for communications security, because Eve can replace both the
hash code and the message that Bob receives, but
they are an essential element of digital signatures.
In this section, we explain how hashing algorithms work, and provide
some practical insight into choosing a suitable algorithm for your
project.
1. Creating a Hash Code
At the
heart of a hashing algorithm is a mathematical function that operates
on two fixed-size blocks of data to create a hash code, as shown in
Figure 1.

We break up Alice's message into blocks that are the
same size as the input for the hash function. The size of each data
block varies depending on the algorithm but the blocks tend to be
small—the algorithms included in the .NET Framework break the
messages into blocks of 512 or 1024 bits. The design of the hash
function differs for each hashing algorithm, but they all share the
same basic approach.
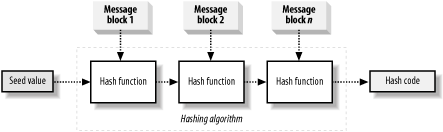
The algorithm specifies a "seed"
value that feeds into the hash function
along with the first block of message data, thus producing our first
hash code. Take this hash code and feed it into the hash function
along with the second block of message data, creating a second hash
code. Feed the second hash code into the function along with the
third message block, and repeat the process of hashing a data block
along with the hash code of the previous block until you have
processed all of the message data, as shown in Figure 2.
The idea of a hash code acting as a message
"fingerprint" is reasonable,
because making even the smallest change in the message data changes
the value of the final hash code. By
"chaining" repeated calls to the
hashing function, you can create a hash code that relies on the value
of every single bit of the message. The output of hashing the first
data block becomes an input to the next operation, which will alter
the value of the second hash code, which will affect the result of
the third operation, and so on. Known as a "ripple
effect" or an
"avalanche," the huge impact that
the smallest change has on the final hash code provides the
fingerprint. Two messages that differ by a single bit of data produce
very different hash codes.
It is important not to confuse the hashing algorithm with the
hash function. The hash function
generates a hash code by operating on two blocks of fixed-length
binary data. The hashing algorithm describes the process of using the
hash function to create a hash code for a message—the algorithm
is a protocol for using the hash function, specifying how the message
will be broken up and how the results from previous message blocks
are chained together.
2. Message Limits
There is limit to the size of message that a
hashing algorithm can process before the hash code is no longer
secure. A very large message causes the initial bytes of message data
to have less of an effect on the hash code than the bytes at the end
of the message. This means that it is easier for Eve to find a
message with the same hash code as Alice sent to Bob, because we have
increased the likelihood of being able to find two messages with
slightly different initial bytes that result in the same hash code.
The problem arises because the hash function is called so many times
for large messages—for example, a 1 GB message will cause the
hash function to be called more than 6,000,000 times. So many hashing
operations lessen the "ripple
effect."
Most hashing algorithms impose a message size limit of
264 bits. This limit is not a practical
consideration for most projects but can be an issue when calculating
hash codes for data generated over a long period. Some algorithms are
able to process 2128 bits of data
securely.
All of the hashing algorithms in the .NET Framework can handle
message limits of at least 264 bits, which
is sufficient for most projects. However, we recommend that you bear
the limit in mind when considering hashing algorithms provided by
third parties.
3. Hash Code Length
It is common to refer to a hash code as
"uniquely" identifying a message,
but the reality is slightly different. The reason that hash codes can
be used to protect message integrity is that it is very difficult
(but not impossible) to find another message that produces the same
hash code.
Irrespective of the size or content of the message processed, hash
algorithms produce a fixed-length hash code, meaning that there is a
finite set of hash code values. We measure the length of a hash code
in binary bits, meaning that a 64-bit hash code can represent
264 different numeric hash values.
You can create an infinite number of different messages, and there
are only a finite number of possible hash codes; therefore, it must
be possible to find a pair of messages that produce the same hash
code. In this section, we consider the security of a 64-bit hash code
which was, until quite recently, thought of as very secure.
For Eve to find a message that produces the same hash code that Alice
has sent to Bob, we expect that she will have to create and test
264 (18,446,744,073,709,551,616) different
messages before she finds a match (assume that hash codes are evenly
distributed). If Eve can check 50 messages per second (around what
you can achieve using our desktop PCs), then it will take her 11.6
billion years to test enough messages. If Eve were able to access
very powerful computers, she might be able to check 10 million
messages each second, but we would still expect her to take 58,494
years to find a match. This is the basic security of hash codes;
realistically, Eve cannot wait almost 60,000 years, meaning that
finding a matching message for a specific hash code is
"computationally
infeasible"—a phrase that is used by
cryptographers to mean "possible, but extremely
unlikely."
However, if Eve can control the contents of both messages, then she
has a much easier job of finding two matching hash codes, known as a
message collision. If Eve wants to
find any pair of messages that create the same
hash code, then she only has to create and test
232 different messages before she has a
better than 50% chance of finding two that match. In fact, if she is
able to check 50 messages a second, she is likely to find a match in
less than 3 years, which is a lot less than the 11.6 billion years it
would take to handle 264 messages. If Eve
is able to check 10 million messages per second, she is likely to
find a pair of messages in a little over 7 minutes.
Eve now has a pair of messages that she has written, both of which
result in the same hash code. She cannot use these messages to bother
Alice and Bob, because she is unlikely to get Alice to hash either of
her messages and send them to Bob. However, Eve can use the following
attack to defraud Joe, who happens to owe her some money:
Eve creates two versions of a message. The first message instructs
Joe's bank to pay Eve $100, which is the amount he
owes her. The second message instructs Joe's bank to
pay Eve $1,000,000.
Eve generates 232 variations of the
innocuous message by making minor editorial changes that do not
affect the meaning of the message (for example, adding spaces or
tabs, or altering the formatting).
Eve also generates 232 variations of her
dishonest message. Because she is in control of the content of both
messages, the chances of her finding a version of the innocuous
message and the dishonest message with the same hash code are better
than 50%.
Eve sends the innocuous message to Joe, who creates a hash code and
digitally signs it. Joe sends the signed hash code
to Eve so that she may present the signed message to his bank.
Eve presents her dishonest message to Joe's bank
along with the signed hash code. The bank checks the digital
signature and finds that the hash code matches the message and that
Joe signed it. Eve was able to forge a signature without learning
Joe's secret keys.
Luckily, for Joe at least, most banks would not honor a request for a
million dollars in this way. Nonetheless, Eve was able to create a
forged message with very little effort—in fact, if Joe has used
a 64-bit hash code for his signature, it would have taken Eve
somewhere between 7 minutes and 3 years to create the messages.
Looking for collisions in this way is a
"birthday"
attack and drastically reduces the
effectiveness of a hashing algorithm, forcing you to treat a hash
code as though it was only half of its actual length.
|
How many people must be in a room before the probability of one of
them sharing your birthday is greater then 50%? The answer is 183.
How many people have to be in the room before the probability of
any two people sharing the same birthday is
greater than 50%? The answer is 23. It is easier to find any shared
birthday than to find a specific one.
Eve is relying on being able to create two messages that produce the
same hash code, knowing that it is simpler than trying to find a
match for a specific message from Alice. Any attack along these lines
is a "birthday attack."
|
If this kind of attack is possible in your project, then you will
need to select an algorithm that creates hash codes with twice the
length you might expect. If this kind of attack is not possible, then
you should select a hash code based on its actual length. As a rule,
a longer hash code will take more time to attack, but takes longer to
generate.
4. The .NET Framework Hashing Algorithms
The .NET Framework includes classes for five
different hashing algorithms, although four of them are closely
related, being variations of the same basic premise to create hash
codes of different length. Table 13-1 lists the
hashing algorithms available.
Table 1. Summary of .NET Framework hashing algorithms
|
Name
|
Input block size
|
Message limit (bits)
|
Hash code size (bits)
|
|---|
|
MD5
|
512
|
264
|
128
|
|
SHA-1
|
512
|
264
|
160
|
|
SHA-256
|
512
|
264
|
256
|
|
SHA-384
|
1024
|
2128
|
384
|
|
SHA-512
|
1024
|
2128
|
512
|
Developed in 1991, MD5 has been used in all sorts of
systems and is an integral part of many standards for communications
security. MD stands for "Message
Digest," and MD5 was the fifth such algorithm that
Rivest had designed.
MD5 is the fastest hashing algorithm included in the .NET Framework,
but the relatively small hash code size makes it more susceptible to
brute force and birthday attacks.
The National Security Agency (NSA) designed the
Secure Hash Algorithm (SHA) in 1993,
and the National Institute of Standards and Technology (NIST)
published it as Federal Information Processing Standard (FIPS) 180,
permitting its use in government projects. NSA withdrew the standard
shortly after publication, replacing it with SHA-1, which contained a
slight modification to the hash function.
The NSA stated that the change addressed a flaw in the original
algorithm that reduced its cryptographic security. The NSA has never
described this flaw, leading the paranoid world of cryptographers to
spend many thousands of hours analyzing the algorithm, looking for
any weaknesses deliberately introduced into SHA-1 to facilitate
government skullduggery. To date, no weaknesses have been found, and
SHA-1 is considered a secure algorithm.
NIST published FIPS 180-2 in 2001, which defined the SHA-256,
SHA-384, and SHA-512 algorithms, named after the length of the hash
code that each produces. These new algorithms are variations of
SHA-1, but are sufficiently recent that their cryptographic security
remains open.
Consider how much you know about an algorithm before selecting one
for use in a project. For example, although SHA-256, SHA-384, and
SHA-512 have longer hash codes, MD5 and SHA-1 are tried and tested
and are known to be reliable. Remember that a longer hash code does
not provide greater security if the underlying algorithm is flawed.